БИОМЕТРИЧЕСКОЕ ИЗУЧЕНИЕ СОРТОВ ГЕЛЕНИУМА ОСЕННЕГО [1977 - - Интродукция и приемы культуры цветочно-декоративных растений]

Многочисленные факты корреляционных связей между различными морфологическими и физиологическими признаками в литературе обычно приводятся как единичные случаи или попутные второстепенные наблюдения на очень небольшом числе повторностей. Поэтому представляет интерес количественное изучение морфологических зависимостей на репрезентативной совокупности особей одного полиморфного вида, охватывающей достаточно полно разнообразие видовых признаков. Наибольшие отклонения от признаков типа обычно наблюдаются среди культивируемых форм вида, главным образом у декоративных растений. Таким образом, совокупность сортов какого-либо декоративного вида, свободного, насколько это возможно, от гибридизационных влияний, можно считать наиболее подходящим объектом для количественного изучения изменчивости некоторых видовых признаков. Такого рода совокупности являются также подходящим объектом для изучения корреляционных связей, ибо, чем более широко охвачен диапазон изменчивости признаков в однородной совокупности, тем более детально и полно удается выявить взаимосвязи между ними.

Из объектов, имевшихся в нашем распоряжении, наиболее полно отвечала поставленным условиям коллекция сортов гелениума осеннего.

С 1967 по 1970 г. на коллекционном участке малораспространенных травянистых многолетников отдела цветоводства Главного ботанического сада АН СССР (Москва) у 22 сортов Helenium autumnale L. измеряли четыре признака: высоту растений, число соцветий и побегов на них, диаметр соцветий. Данные затем были обработаны методами математической статистики. Указанные четыре признака измеряли в двух состояниях растений: после пересадки (1967, 1969, 1970 гг.) и без пересадки — в 1968 г. Во всех случаях растения пересаживали и делили весной, а все признаки измеряли в середине сентября, так как большинство сортов гелениума осеннего цветет с начала августа по конец сентября, в чем заключается их большая декоративная ценность. Изучение явлений возмещающей изменчивости или компенсационных модификаций облегчает понимание взаимосвязей в комплексе признаков организма. Представляют интерес возможности регулирования соотношения между вегетативной и репродуктивной массами у возделываемых растений. В частности, если ведется отбор для получения сорта с крупными цветками, то полезно иметь в виду, что изменение диаметра цветков зависит и от высоты растений. Разнообразные примеры подобных зависимостей были приведены ранее [1].

Сравнительный анализ видовых и сортовых признаков гелениума показал их неустойчивость в зависимости от условий среды. Так, два сорта могут в одном году достоверно различаться друг от друга, например, по высоте растений, а в другом году они по этому признаку не различаются.

Корреляционные связи являются отражением более глубоких причинных взаимосвязей жизненных функций организма, и в этом отношении они — более устойчивые и постоянные признаки, принадлежащие по таксономическому рангу к родовым или даже признакам семейства. Конечно, это касается не столько арифметической величины показателей, сколько направлений и типа связи.

Исследовали корреляционные взаимосвязи между четырьмя признаками гелениума осеннего: высотой растений, числом соцветий, диаметром соцветий и числом побегов на одном растении. С этой целью вычисляли парные коэффициенты корреляции, прямые и обратные корреляционные отношения и показатели корреляции рангов, а также частные коэффициенты корреляции, в зависимости от особенностей экспериментального материала и цели обработки. Некоторые, наиболее характерные эмпирические зависимости были аппроксимированы главным образом по уравнению параболы второй степени.

Признаки растения обычно связаны в единый комплекс, или плеяду взаимосвязей, поэтому выявление парных взаимосвязей имеет самостоятельное практическое значение лишь тогда, когда эти связи сильно выражены. В большинстве случаев показатели парных связей целесообразно вычислять лишь для их последующего анализа методами множественной корреляции, например путем вычисления частных коэффициентов корреляции, благодаря которым нередко удается выявить более полную структуру взаимосвязей комплекса признаков, что представляет собой наиболее ценный и большей частью конечный результат подобных исследований. Поэтому обсуждаемые ниже в пунктах I—VI парные взаимосвязи следует рассматривать в основном как этап, необходимый для перехода к изучению структуры взаимосвязей.

Далее рассматриваются четыре аспекта корреляционных взаимосвязей высоты растений и числа соцветий:

1) выявление связи между а: и у на растениях после деления в совокупности сортов по учету 1967 г.; 2) выявление связи между х и у на неделившихся растениях в совокупности сортов по учету 1968 г.; 3) та же связь, но на трех отдельных сортах, чтобы исключить влияние общего фона смешанной совокупности сортов; 4) попутно получены данные о степени индивидуализации вертикальных побегов, идущих от шейки корня, и правомерности холистического или мерологического подхода к этим побегам и особи гелениума; с этой целью в 1967 г. соцветия подсчитывали на каждом отдельном побеге, идущем от шейки корня, а в 1968 г. число соцветий учитывалось в целом по растению.

1. Осенью 1967 г. было подсчитано число соцветий указанным способом на 434 побегах, относящихся к 15 сортам. Так как во взаимосвязях между высотой растений и числом цветков на них не всегда бывает ясно, какой из этих двух признаков является причиной или аргументом, то вопрос о направлении взаимосвязи в данном случае был решен при помощи вычисления прямого и обратного корреляционных отношений. Данные измерений 434 побегов гелениума сведены в корреляционную решетку (табл. 1), где приводятся также значения эмпирических линий регрессии: у/х и я/у, необходимые для вычисления корреляционных отношений и уравнений парабол. Оба корреляционных отношения — прямое (η_x/y=0,435) и обратное (η_y/x=0,427) достоверны даже по доверительному уровню Р_з'=0,999, что служит указанием на сильную связь между высотой растений и числом соцветий на них.

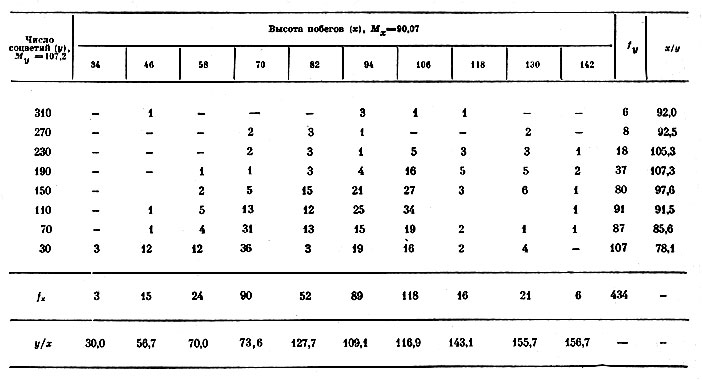
Таблица 1. Распределение 434 вертикальных побегов гелениума осеннего по высоте (в см) и числу соцветий на них (1967 г.)

Поскольку соответствующее корреляционное отношение по величине больше (0,435>0,427), заключаем, что высота побегов больше зависит от числа соцветий на них, чем наоборот — число соцветий от высоты растений. Следовательно, в рассматриваемой парной взаимосвязи число соцветий — аргумент, а высота побегов — функция.

Зависимость числа соцветий от высоты растений и обратная зависимость — высоты растений от числа соцветий — аппроксимированы параболой второй степени по способу наименьших квадратов (в скобках указана ошибка уравнения):

в этих уравнениях: у — число соцветий, х — высота растений.

Рис. 1 дает представление о зависимости высоты побегов от числа соцветий на них. Двускатная линия регрессии достигает максимума, после которого с дальнейшим увеличением числа соцветий высота побегов уменьшается. Снижение высоты побега происходит тогда, когда на нём появляется свыше примерно 200 соцветий. Таким образом, взаимосвязь двух признаков: высоты побегов и числа соцветий на них — имеет вид двускатной кривой, что согласуется с данными, полученными на других растениях [1].

2. Осенью 1968 г. число соцветий на 270 особях гелениума подсчитывалось в целом на растении, чтобы выяснить, в каком случае связь между числом соцветий и высотой растений будет выступать яснее: при суммарном учете соцветий по каждой особи или на каждый вертикальный побег, отходящий от шейки корня (как это было проделано в 1967 г.). Ответ на поставленный вопрос может также служить и указанием на степень индивидуализации вертикальных побегов в процессе их обособления в отдельные растения. В табл. 2 приведены данные этих измерений в форме корреляционной решетки, где у/х и х/у — значения прямой и обратной линий регрессии.

Руководствуясь графиком эмпирической линии регрессии (сходным с таковым на рис. 1), можно заключить, что зависимость числа соцветий от высоты растений также двузначная, т. е. близка к параболической, во всяком случае она может быть передана двускатной кривой регрессии. Коэффициент корреляции для рассматриваемой связи оказался равным: r=+0,26, а прямое корреляционное отношение η=0,30, оба показателя достоверны по самой строгой оценке.

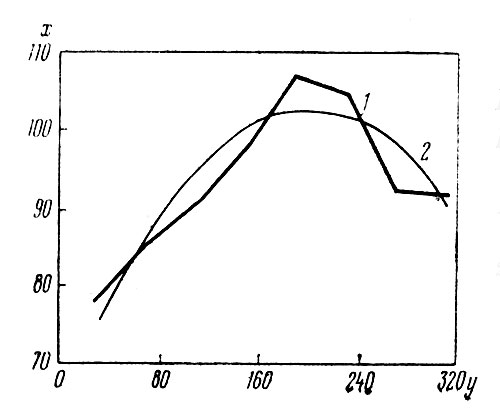
Рис. 1. Зависимость высоты растений (х) от числа соцветий (у) на них: 1 — эмпирическая линия регрессии; 2 — ее аппроксимация параболой второй степени

Графический анализ указанной зависимости показал, что максимальное число соцветий на одном кусте гелениума (485) достигается при высоте растения примерно 163 см.

3. Незначительное различие обоих показателей корреляции по величине в только что рассмотренном случае означает не то, что связь может быть выражена прямой линией, а то, что связь между признаками неясно выражена из-за каких-то мешающих факторов.

Принимая во внимание расположение частот в корреляционной табл. 2, мы можем также заметить, что связь между высотой растений и числом соцветий на них в целом выступает нечетко. Одной из причин этого может быть неоднородность изучаемой совокупности, состоящей из 15 сортов гелениума. Поэтому та же взаимосвязь была рассмотрена в отдельности по каждому из трех сортов, коэффициент корреляции между высотой растений и числом соцветий у которых, по данным 1968 г., был равен у: 'Moerheim Beauty': r=0,90±0,06; 'Cranatstern': r=0,64±0,12; 'Biedermeier': r=0,52±0,10.

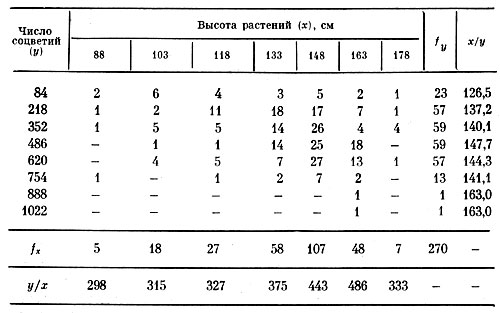
Таблица 2. Распределение 270 особей гелениума по высоте и числу соцветий на них (1968 г.)

Все три приведенных коэффициента корреляции достоверны не менее чем на 95% уровне значимости и по величине значительно больше, чем полученные выше по смешанной совокупности из 15 сортов, представленных 270 особями (r=0,26; η=0,30). Таким образом, действительно в более однородной выборке, т. е. в пределах сорта, взаимосвязь признаков проявляется более четко. У всех трех сортов в пределах конкретных данных эта связь графически сходная и положительная: чем больше высота растений, тем больше на них соцветий. Эмпирические линии регрессии аппроксимированы следующими уравнениями параболы второй степени (в том же порядке сортов):

которые вычислены по методу наименьших квадратов (рис. 2).

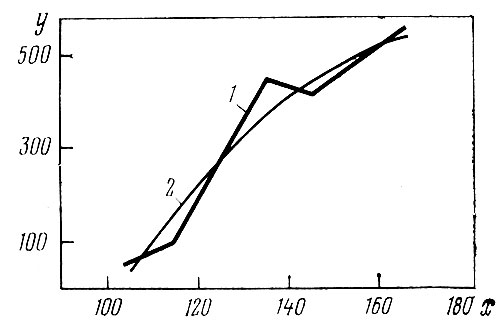
Рис. 2. Зависимость числа соцветий (у) от высоты растений (х) у сорта 'Biedermeier' (1968): 1 — эмпирическая линия регрессии; 2 — ее аппроксимация параболой

4. Если число соцветий подсчитывалось в отдельности на каждом вертикальном побеге, корреляционные отношения между числом соцветий и высотой побегов были 0,435 и 0,427, как это видно в пункте 1 по данным 1967 г. Показатель корреляции рангов для среднесортовых данных по тем же признакам за 1967 г. равен: ρ_xy=+0,56.

Если же число соцветий учитывалось в целом на растении, как это дано в пункте 2 по данным 1968 г., то связь между высотой растений и числом соцветий на них становится слабее: коэффициент корреляции r=+0,26, а корреляционное отношение η=30. Из этого следует, что вертикальные побеги, отходящие от шейки корня у гелениума, по-видимому, в большей степени отдельные растения, чем компоненты единой особи.

II. Высота растений (х) — диаметр соцветий (z). Между высотой растений и диаметром соцветий, по-видимому, существует слабая корреляционная связь, на что указывает величина коэффициента корреляции рангов по Спирмену, которая для средне-сортовых данных за 1967 г. равна ρ_xy=0,21, что не является, однако, достоверным значением. Коэффициент корреляции оказался также недостоверным для тех же данных: r=0,12, его ошибка с преобразованием через z по Фишеру m_z=0,28. Возможно, что выявлению парной взаимосвязи между х и z в данном случае мешает влияние двух других признаков, что будет рассмотрено далее.

III. Высота растений (х) — число побегов (u). Зависимость высоты растений от числа побегов на них у гелениума в целом по совокупности сортов по измерениям 1967 г. представлена в табл. 3, по данным которой вычислено уравнение, аппроксимирующее эмпирическую линию регрессии на рис. 3: х = 83,037 + 7,4550u - 1,3657u².

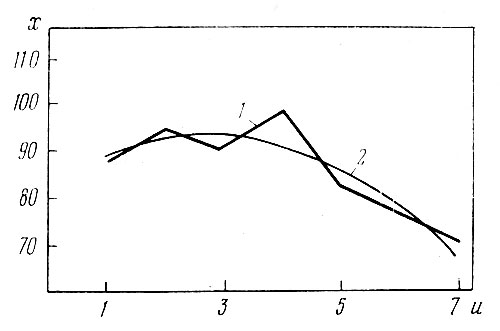
Рис. 3. Зависимость высоты растений (х) от числа побегов на них (и): 1 — эмпирическая линия регрессии; 2 — ее аппроксимация параболой

Несмотря на то что теоретическая линия регрессии (рис. 3,2) удовлетворительно совпадает с эмпирической кривой (рис. 3,1), в данном случае показатели связи не вычисляли, так как х=7, что недостаточно (табл. 3) для суждения о корреляции. Поэтому лишь рис. 3 может дать примерное представление о типе связи между высотой вертикальных побегов осенью и их числом на одну особь гелениума у растений, которые делились весной этого же года.

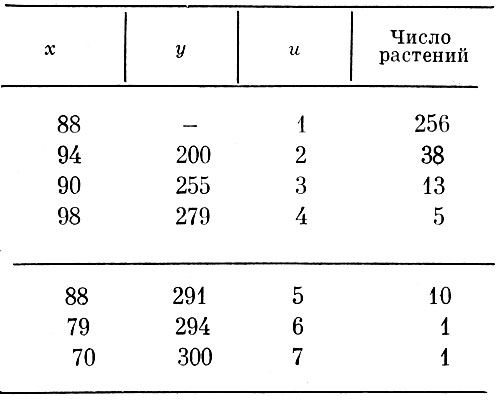
Таблица 3. Высота растений в см (х), число соцветий (у) и число побегов (и) на них (1967 г.)

У растений, которые в течение двух лет не делились, связь между числом побегов и высотой растений по совокупности сортов изучалась на данных измерений 269 особей осенью 1968 г. По частотам корреляционной решетки (в работе не приводится) были вычислены: квадраты коэффициента корреляции r²=0 и прямого корреляционного отношения η²_u/x=0,03, критерий криволинейности — F=1,62. Все эти показатели были недостоверными. По-видимому, в смешанной совокупности сортов начинают сильнее проявляться специфичные сортовые особенности, которые создают фон отклонений, значительно мешающий проявлению общей закономерности. Поэтому зависимость между числом побегов и высотой растений была рассмотрена в отдельности по каждому из трех сортов, данные по которым получены в том же 1968 г.

Для выяснения, какой признак в этой парной связи считать ведущим, или аргументом, был применен следующий метод. Как известно, точки эмпирической линии регрессии можно вычислить двумя способами: u/х или х/u [2], в первом случае за аргумент принимается х, во втором и в соответствующей зависимости от большей величины показателя связи. Вначале были вычислены сочки эмпирических линий регрессии u/х; между ними (число побегов) и рядами х (высота растений) коэффициенты корреляции г и их ошибки у трех сортов оказались следующими: r=0,37±0,11, (N=69); 'Granatstern3 r=0,44±0,14 (N=45); 'Moerheim Beauty' r=0,18±0,14 (N=48), где N — объем выборки, т. е. число растений.

Достоверны коэффициенты корреляции лишь у первого и второго сортов, у третьего сорта величина коэффициента корреляции незначима, в целом же зависимость числа побегов, представленного точками эмпирической линии регрессии u/х от высоты растений (х), не очень сильная.

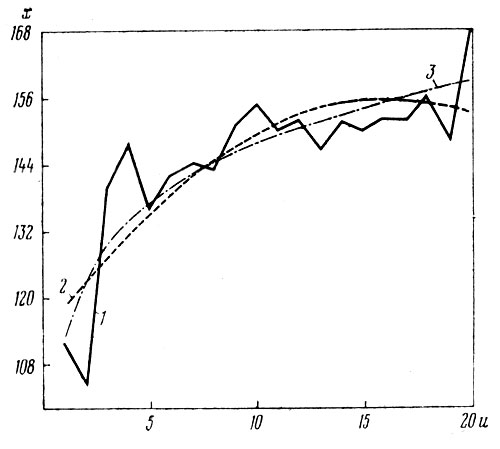
Рис. 4. Зависимость высоты растений (х) от числа побегов (u) у сорта 'Briedermeier': 1 — эмпирическая линия регрессии; 2 — аппроксимация ее параболой; 3 — аппроксимация по уравнению х=112,87 + 15,219 Ln(u)

Графики зависимости u/х от х, построенные для всех трех сортов (в работе не приводятся), также показали, что в этом случае, когда х принят за аргумент, связь выражена неясно, четкой тенденции в ходе кривых не выявляется. При вычислении точек обратной эмпирической линии регрессии, т. е. х/u, когда за аргумент принято число побегов, были использованы данные лишь по первому сорту, так как у него связь между u/х и х оказалась более выраженной, чем у других двух сортов; по уравнению параболы второй степени: х=113,45+5,2338u -0,1625u²(±8,6). На рис. 4 изображены эмпирическая линия регрессии (1) и выравнивающая ее парабола (2). Из рис. 4, 2 видно, что максимальной высоты растения этого сорта достигают, когда они образуют 16 побегов, при дальнейшем усилении ветвления высота растений снижается. Несколько лучшее приближение, особенно в начале кривой, дает уравнение х'=112,82+35,093lg(х) или х'=112,87+15,219In(х) (рис. 4,3).

Коэффициент корреляции между высотой растений х/u и числом побегов на них для сорта 'Biedermeier' (табл. 4) достоверен и равен r=0,75, показатель корреляции рангов Спирмэна для этих же данных тоже достоверен: ρ=0,80. Так как во втором варианте вычисления эмпирической линии регрессии (х/u) взаимосвязь графически выявляется значительно лучше, а величина показателей связи повысилась, то аргументом здесь можно считать число побегов, от которого высота растений зависит более, чем наоборот.

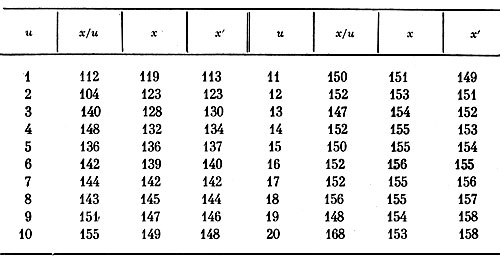
Таблица 4. Зависимость высоты растений (х/u) от числа побегов на них (u) у сорта

IV. Число соцветий (у) — диаметр соцветия (z). Корреляция между этими двумя признаками по средним для 15 сортов данным за 1967 г. оказалась недостоверной (ρ_yz=0,07). Эта взаимосвязь более подробно рассматривается далее в комплексе с другими признаками.

V. Число соцветий (у) — число побегов (u). По данным измерений в 1968 г., в котором растения не делили, составлена корреляционная решетка для решения вопроса об аргументе и вычислены эмпирические линии регрессии прямой и обратной связи (у/u, u/у). По схеме полного корреляционного анализа [3], по данным табл. 5, были вычислены: r²=0,30; F_Т²=71,6; η²=0,42; F_η²=7,04; критерий криволинейности F=2,09. При числе степеней свободы ν₁=23—2=21, ν₂=269—23=246, на 95%-ном уровне достоверности связь между признаками считается криволинейной. При ν₁=1, ν₂=269-2=267 и ν₁=23-1=22; ν₂=269-23=246 квадраты коэффициента корреляции и корреляционного отношения достоверны на всех трех стандартных уровнях значимости. Считая за аргумент строку и и за функцию строку у/u из табл. 5, по способу наименьших квадратов вычислили коэффициенты уравнения параболы второй степени:

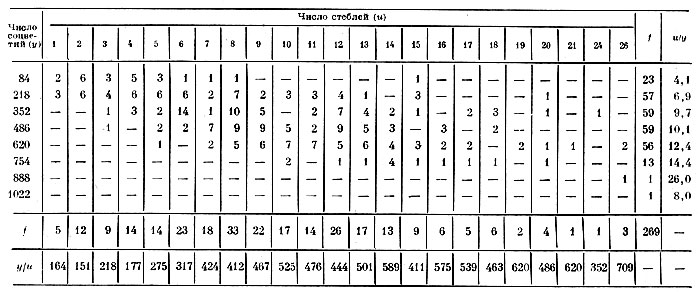
Таблица 5. Число побегов и соцветий на растении в 1968 г. (без деления и пересадки)

Анализ этого уравнения показывает, что наибольшее число соцветий (y=552) на неделившемся растении гелениума достигается при числе побегов на нем u=19, максимальное число побегов может достигать u=38. Аппроксимирующая линия регрессии числа соцветий в зависимости от числа побегов вычислена по приведенному уравнению параболы и представлена на рис. 5.

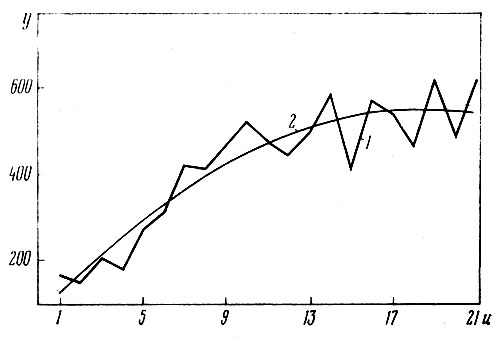
Рис. 5. Зависимость числа соцветий (у) на растении от числа побегов (и): 1 — эмпирическая линия регрессии; 2 — аппроксимация ее параболой

Таким образом, число соцветий на растении в сильной степени зависит от числа побегов на нем. Обратная зависимость — числа побегов от числа соцветий — выражается менее ясно и подтверждает то, что в данной взаимосвязи за аргумент следует принимать число побегов, как это было установлено графически и аналитически (графики и расчеты в работе не приводятся).

Зависимость числа соцветий от числа побегов у разных сортов различается по силе корреляции:

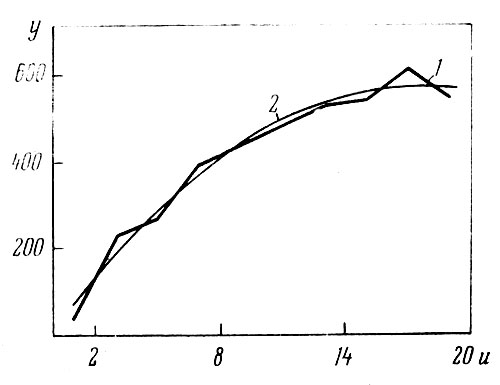
Рис. 6. Зависимость числа соцветий (у) от числа побегов (и) на растении у сорта 'Biedermeier' (1968 г.): 1 — эмпирическая линия регрессии; 2 — ее аппроксимация параболой

Тип параболической зависимости, как видно из рис. 6, при этом сохраняется. Эмпирическая линия регрессии на рис. 6 аппроксимирована уравнением:

из которого видно, что максимальное число соцветий у сорта 'Biedermeier' бывает при 17 побегах на одном растении.

Сходный тип зависимости установлен и у других двух сортов (графики и уравнения здесь не приводятся).

Все установленные выше (см. пункт V) факты относятся к неделившимся растениям. Однако графически достаточно четко та же зависимость выступает и на совокупности растений всех изучаемых сортов по данным 1967 г., когда растения делили (табл. 3 и рис. 7), хотя число побегов на делившихся растениях в целом бывает небольшим и габитус растения недостаточно выражен.

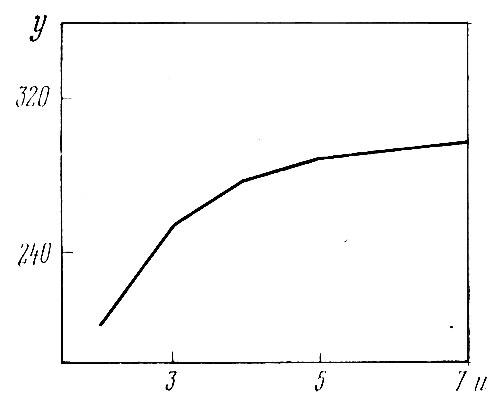
Рис. 7. Зависимость числа соцветий (у) от числа побегов (и) на растении (1967 г.), эмпирическая линия регрессии

VI. Диаметр соцветий (z) — число побегов (и). По среднему диаметру цветков и числу побегов на одном растении гелениума каждого сорта за 1968 г. вычислен коэффициент корреляции между этими признаками. При N=15 сортов, r=—0,83; вычисленный коэффициент корреляции достоверен, верхняя и нижняя границы его доверительного интервала соответственно равны -0,95 и -0,51.

Коэффициент корреляции между этими же признаками, по данным 1967 г., r=—0,089, его ошибка m_r=0,28, т. е. связь отсутствует. Объясняется это различие тем, что в 1968 г. растения не делили, поэтому они имели хорошо разветвленную наземную часть. В 1967 г. после деления кустов на большинстве растений было по 1—2 побега и, вследствие малого варьирования числа побегов, связь не могла быть выявлена.

Таким образом, установленная отрицательная величина коэффициента корреляции свидетельствует о том, что сильное развитие вегетативной массы растения гелениума ведет к измельчению находящихся на нем соцветий и, следовательно, к некоторому снижению его декоративности. Поэтому деление растений гелениума с пересадкой поддерживает их декоративность в цветущем состоянии и является эффективным агротехническим мероприятием, биологическим обоснованием которого может служить установленный здесь факт обратной взаимосвязи между числом побегов на растении и диаметром находящихся на нем соцветий.

VII. Множественные корреляции. Факт тесной взаимосвязи как морфологических, так и физиологических признаков у растений, хотя давно уже не нов, на практике еще почти не используется. Одной из причин этого, по-видимому, является то, что сила таких взаимосвязей во многих случаях количественно не оценивается, между тем как корреляционные связи между признаками растения далеко не равнозначны и без числового выражения силы этих связей невозможно объективно выделить главные и второстепенные из них.

В работе по выведению новых сортов путем селекции важно знать, каким образом сопряжены их признаки, чтобы предусматривать результаты отбора. Если, например, желательно усилить какой-то признак А, то при этом, возможно, придется мириться с неизбежным ослаблением какого-то признака Б или, напротив, с параллельным усилением некоторого признака В. Поэтому любой основательной селекционной работе должно предшествовать изучение комплекса корреляционных связей между важнейшими признаками у данного вида на совокупности его сортов или географических рас, т. е. на максимально разнообразной выборке.

Структура взаимосвязей признаков рассмотрена на следующих трех группировках объекта с применением различных методов биометрии:

1) у растений после их деления, на данных 1967 г., когда число соцветий подсчитывалось отдельно на вертикальных побегах, отходящих от шейки корня;

2) по усредненным данным за три года: 1967, 1969, 1970, когда растения также делили;

3) у растений, не делившихся два сезона, по данным 1968 г. 1. Для изучения взаимосвязей трех признаков в комплексе у растений после деления по каждому сорту гелениума по измерениям 1967 г. были вычислены средние арифметические по высоте растений, числу соцветий на одном растении и диаметру соцветий (данные не приводятся). Вычисление показателя корреляции рангов по Спирмэну выяснило, что существует достоверная положительная корреляция между высотой растений и числом соцветий на них: ρ_xy=0,56. Однако корреляция между высотой растений и диаметром соцветий на них ρ_xz=0,21, а также между числом соцветий и их диаметром ρ_yz=0,07 осталась недоказанной.

Существенно не изменило полученной структуры связей и вычисление частных показателей корреляции рангов, которые равны: ρ_xy•z=0,56; ρ_xz•y=0,21; ρ_zy•x=—0,06; общий коэффициент связи трех признаков R_y•xz=0,56.

Как было установлено выше, все рассмотренные парные взаимосвязи обладают той или иной степенью криволинейности. Хотя показатель корреляции рангов по сравнению с обычным коэффициентом корреляции способен отражать в несколько большей степени криволинейность связи, однако он по своей конструкции может надежно отразить лишь прямолинейную связь, что в рассматриваемом случае и могло повлиять на величину показателей связи.

Обработка более полных данных за тот же год произведена поэтому далее двухфакторным дисперсионным анализом, который выполнен в двух вариантах.

В первом варианте в качестве объекта берется диаметр соцветий, на который действует фактор 1 — высота растений в см и фактор 2 — число соцветий; в анализе участвовало 150 растений (15 сортов). В табл. 6 приводятся результаты дисперсионного анализа по первому варианту. Сравнение полученных дисперсий с остаточной (σ²_ост=0,834) показывает, что на диаметр соцветий достоверно влияет высота растений (фактор 1), так как вычисленный критерий Фишера F больше табличного (13,772>3,07) на уровне достоверности P₁=0,95. Влияние числа соцветий (фактор 2) на их диаметр не доказано, поскольку фактический критерий F меньше табличного (4,508<254,3). Достоверное влияние оказывают оба фактора на диаметр соцветий и в их взаимодействии (8,398>3,07), по-видимому, главным образом за счет фактора 1 — высоты растений. Большая часть варьирования диаметра соцветий вызывается не факторами 1 и 2, а другими неучтенными причинами, так как доля остаточной дисперсии значительна —76,38%, остальная часть варьирования 23,62% возникает в результате действия учтенных факторов 1 и 2.

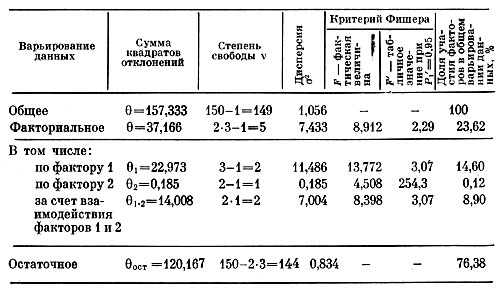
Таблица 6. Результаты двухфакторного дисперсионного анализа (фактор 1 — высота растений, фактор 2 — число соцветий)

По второму варианту обработки данных дисперсионным анализом за объект опыта принята высота растений, на которую действуют фактор 1 — число соцветий на растении и фактор 2 — диаметр соцветий в мм. В табл. 7 сгруппированы опытные данные 140 особей по градациям и часть вычислений, в табл. 8 дана оценка значимости факториальных дисперсий.

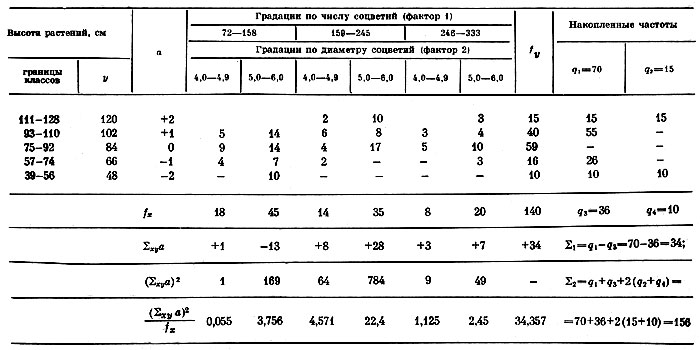
Таблица 7. Комбинационная таблица двухфакторного дисперсионного анализа данных по влиянию на высоту растений числа соцветий и диаметра соцветий

Таким образом, взаимосвязи в совокупности сортов у делившихся растений в комплексе трех признаков изучались по данным 1967 г. при помощи двухфакторного дисперсионного анализа, в первом варианте которого в качестве объекта служил диаметр соцветий, а факторами были высота растений в см и число соцветий на них. При этом оказалось, что на диаметр соцветий достоверно влияет высота растений, влияние числа соцветий на их диаметр не доказано. Достоверно влияют оба фактора на диаметр соцветий и во взаимодействии (y∩x). Во втором варианте дисперсионного анализа выяснилось, что на высоту растений достоверно влияет число соцветий, а диаметр соцветий не оказывает заметного действия на высоту растений. На рис. 8, с учетом связей, выявленных вначале, показана структура перечисленных взаимосвязей трех признаков. Совместное действие признаков, например числа соцветий и их диаметра, на рисунке обозначается так: y∩z. Следовательно, нужно иметь в виду, что отбор крупноцветковых особей гелениума, когда их делят, не повлечет за собой изменения высоты растений, но отбор высокорослых особей может быть сопряжен с изменением диаметра соцветий, который при этом будет в основном уменьшаться. При отборе обильно цветущих особей, по-видимому, будет наблюдаться уменьшение высоты растений.

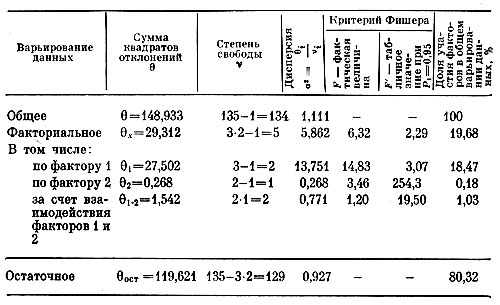
Таблица 8. Результаты двухфакторного дисперсионного анализа (фактор 1 — число соцветий, фактор 2 — диаметр соцветий на тех же особях гелениума)

2. По данным для делившихся растений, которые представляют собой средние по 22 сортам за три года — 1967, 1969 и 1970, были вычислены парные коэффициенты корреляции между тремя признаками: r_ху=0,443, r_xz=0,216, r_yz=0,0608, из которых достоверным на 5%-ном уровне значимости оказался лишь первый из них.

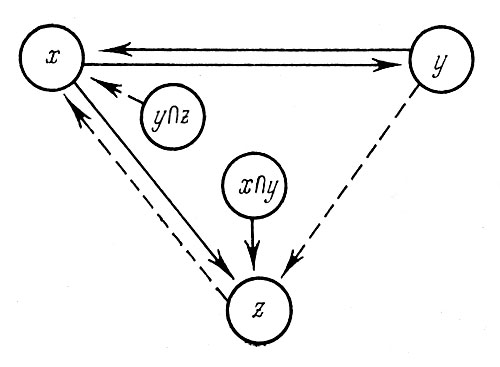
Рис. 8. Достоверные (сплошные линии) и недостоверные (штриховые линии) связи между высотой (x), числом соцветий (y) и диаметром соцветий (z) у делившихся растений гелениума

Вычисление частных коэффициентов корреляции:

r_ху•z=0,441; r_хz•у=0,212; r_yz•х=—0,0402; R_y•хz==0,445 показало, что они не вносят почти ничего нового в структуру связей, которая похожа на установленную ранее. Поэтому не представляется необходимым изучать ее здесь более глубоко. Индекс, отделяемый точкой от остальных индексов, при коэффициентах обозначает, как и всюду в работе, фактор, действие которого на два других исключается.

3. У неделившихся растений гелениума по измерениям 1968 г. рассмотрены множественные корреляции в комплексе четырех признаков: высоты растений (х), числа соцветий на них (у), диаметра соцветий (z) и числа побегов на растении (u). Парные коэффициенты корреляции между этими признаками равны:

Частные коэффициенты корреляции первого и второго порядка вычислялись по рекуррентной формуле [4], они равны:

xy.z 0,139; ху.u 0,248; xz.u 0,035; xz.y —0,0699; хu.у —0,283; xu.z — 0,188; yz.x 0,390; yz.u 0,301; уu.х 0,524; yu.z 0,433; zu.x 0,272; zu.y 0,102; xy.zu 0,249; xz.yu — 0,0429; xu.yz — 0,278 yz.xu 0,302; yu.zx 0,472; zu.xy 0,0862.

В соответствии с последними шестью величинами частных коэффициентов, которые и являются конечными результатами, на рис. 9 представлены связи между четырьмя признаками у неделившихся растений гелениума. Основой структуры служит наиболее сильная положительная связь (0,472) между числом соцветий (y) и числом побегов на растении (u). Число соцветий, таким образом, больше зависит от числа побегов, чем от высоты растений (r_xy.zu= =0,249). Высота растений находится в отрицательной связи с числом побегов (r_xu.yz=—0,278), т. е. чем больше высота растений, тем меньше число вертикальных побегов, из которых они состоят. Влияние высоты растений на диаметр соцветий опосредовано его положительной связью с числом соцветий (r_yz.xu=0,302), т. е. увеличение диаметра соцветий в основном происходит с одновременным увеличением числа соцветий. Представленная на рис. 9 структура передает лишь основные тенденции связей, ибо они в той или иной степени криволинейны, как было установлено выше. Поэтому для уточнения формы зависимости следует обращаться к парным зависимостям, рассмотренным выше. Вероятно, в силу своей криволинейности не была отражена, например, реально существующая связь соответствующей величиной частного коэффициента корреляции между диаметром соцветий и числом побегов; возможно также, что эта связь проявляется лишь при совместном действии высоты растений и числа побегов на них, т. е. целиком всей наземной вегетативной части растения. В основном же схема на рис. 9 отражает реально существующие связи между четырьмя признаками и может оказать помощь при выборе направления и плана селекции новых сортов гелениума осеннего.

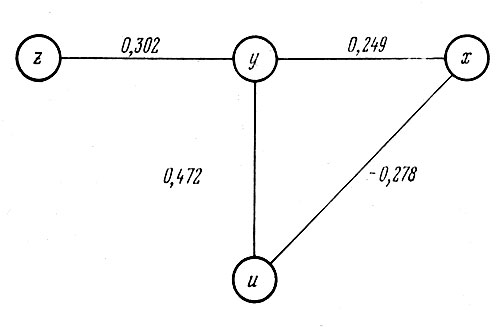
Рис. 9. Структура взаимосвязей между признаками у неделившихся растений гелениума осеннего: x — высота растений; у — число соцветий; z — диаметр соцветий; u — число побегов. Цифры — величины частных коэффициентов корреляции между соответствующими признаками

1. Г. Н. Зайцев. 1967. Применение биометрических методов в изучении явлений возмещающей изменчивости у растений. Л.

2. Г. Н. Зайцев. 1973. Методика биометрических расчетов. М., «Наука».

4. Д. Э. Юл, М. Д. Кендэл. 1960. Теория статистики. М., Госстатиздат ЦСУ СССР.